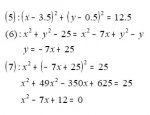Dass das bis heute fertig werden musste, hab ich nicht gewusst, sorry.
Der Kreis hat den Mittelpunkt M bei (0,0), P die Koordinaten (7,1), der Mittelpunkt H des Thaleskreises liegt bei 1/2 * P = (3.5,0.5). Der Radius r des Thaleskreises beträgt (Anhang (1)). H habe ich nun mit der
Drehmatrix R auf die x-Achse gedreht, siehe (2). Frag mich nicht warum, das war einfach nur, weil ich anders nicht weitergekommen bin. Der Winkel ist durch -arctan(0.5/3.5) gegeben. Durch diese Drehung verschieben sich auch die Schnittpunkte der beiden Kreise, was wir später berücksichtigen müssen. Die Gleichung des gedrehten Thaleskreises ist (3). Die beiden Kreise setzt man nun gleich (4), wobei man die beiden Ergebnisse wieder zurückdrehen muss (analog zu (1)), was zu B1=(3,4) und B2=(4,-3) führt. Die Geradengleichungen erhält man jetzt durch Einsetzen.
Wie gesagt, das mit der Drehung kann ich nicht wirklich erklären. Wenn man sich die originalen und gedrehten Kreise und Dreiecke hinzeichnet, sieht man, dass es funktioniert. Hätt ich gern gemacht, aber meine AutoCad-CD mag nicht mehr. Bin mir ziemlich sicher, dass es auch eine wesentlich einfachere Lösung gibt, aber die seh ich irgendwie nich..
Edit: Hier die einfache Lösung: Wie oben bis (1). Wir lassen dann das Drehen *g* und nehmen (5) als Gleichung für den Thaleskreis. Diese wird aufgelöst und mit der Kreisgleichung gleichgesetzt (6), was als Lösung die Gleichung der Geraden durch die beiden Berührungspunkte ergibt. Diese wird in die Kreisgleichung eingesetzt (7). Die quadratische Gleichung ergibt dann die beiden Berührungspunkte.
Die Frage hatte vor genau einem Jahr in nem anderen Forum schon mal jemand gestellt ;-)